Lexical Analysis

Lexical Analysis (Lexer)

• Computer sees a program as a big linear string

what you see

if (i == j) 
  Z = 0;
else
  Z = 1;

what the compiler/computer see

\t|if| |(|i| |==| |j||)|\n\t\tz = 0;\n\telse\n\t\tz = 1;

• Thus the job of the Lexer is to split this big linear string into substrings (tokens or lexemes), and classify them in to token classes.

Token

• Identifier: strings of letters or digits, starting with a letter, A1, Foo, B17
• Integer:
  • non-empty string of digits 0, 12, 001, 00
• Keyword:
  • else or if or begin or ...
• Whitespace:
  • a non-empty sequence of blanks, newlines, and tabs if .... (

• Thus, the lexer takes as input a program (a string) and returns a tuple of token classes and lexemes. Modern compilers, including the one you are developing, also include additional details such as line numbers.

Example

"foo = 42"  --->  LA --->   {(ID, "foo"), (Op, "="), (Num, "42")}

Some challenges in LA

• FORTRAN rule: whitespace is insignificant

  • VAR1 is the same as VA R1
  • DO 5 X = 1,25 (loop) vs DO5X = 1.25 (variable assignment)

• In PL/I keywords are not reserved

  • IF ELSE THEN THEN = ELSE; ELSE ELSE = THEN
  • DECLARE (ARG1,. . ., ARGN): Is DECLARE is a keyword or an array reference?

• C++

  • template syntax: Foo<Bar>
  • stream syntax: cin >> var;
  • nested application of templates Foo<Bar <Barzz>>
    • C++ compiler regards the last >> as stream syntax
    • so programmers need space to distinguish > > (new C++ compilers might not have this issue)

Regular Languages

• Goal: used to determine what token class a substring belongs to

Regular Expression

Each regex defines a language, which is a class or set of string. Moreover, regex are defined over some finite set of characters \(\sigma\), which is called alphabet of the language.

Formally, regex are built up from constant and compound expressions.

Constants:

• \(\emptyset\): represent an empty language, i.e., an empty set
• Single character c: represent a singleton set consisting of just c as a member, i.e., a set of 1 element {c}
• Epsilon \(\epsilon\): represent a singleton set consisting of just `` as a member, i.e., the set of 1 lement {''}

Compounds:: Given a regex \(A\) and \(B\), we can apply the following operators over them to obtain another regex

• Union: \(A + B\) (or \(A \| B\)

  • {"ab", "c"} | {"ab", "d", "ef"} = {"ab, "c", "d", "ef"}

• Concatenation: \(AB\)

  • {"ab", "c"} {"d", "ef"} = {"abd", "abef", "cd", "cef"}

• Iteration: (Kleene star)

  • \(A^* = \bigcup_{i \ge 0} A^i\)
  • \(A^i = A \dots_{i \text{ times }} A\)
  • \(A^0 = \epsilon\)
  • (0+1)* = {"0", "1"}* = {e, 0, 1, 00, 11, 01, 10, ...} # set of all binary string (including the empty string)
  • {"ab", "c"}* = {e, "ab", "c", "abab", "cc", "abc", "cab", ...}

In-class Exercise

Given the regex R1: (0 + 1)*1(0 + 1)*, which of the following regex's are equivalent to R1?

• First, we can try to understand what R1 matches (or accepts or recognizes):

  • R1 accepts: 1, 10, 1000, 01 , 0110101,
  • R1 does not accepts: 0, 00
  • looks like R1 accepts any (binary) string that has at least a 1 in it

• R2: (01 + 11)(0 + 1)

  • Not equiv to R1 (accepts a empty string)
• R3: (0 + 1)(10 + 11 + 1)(0 + 1)
  • Equiv to R1
• R4: (1 + 0)1(1 + 0)
  • Equiv to R1
• R5: (0+ 1)(0 + 1)(0 + 1)
  • Not equiv to R1 (accepts 0)

• Mapping syntax to semantics

  • We use the function L to map from syntax, a regex, to a set of strings (that regex accepts)

  Function L

  • L(\(\epsilon\)) -> {''}
  • L('c') -> {'c'}
  • L(\(\emptyset\)) -> {}
  • L(A + B) -> L(A) \(\vee\) L(B)
  • L(AB) => {ab | a in L(A) \(\wedge\) b in L(b)}
  • L(A\(^*\)) => U\(_{i\ge0}\) L(A\(^i\))

Finite Automata

• We can use RE's to describe various languages (e.g., digits: digit digit*, identifier: letter (letter+digit)\(^*\), reserved keywords: "if" | "then" + "else", ...)
• Regular languages are are language specification
• We now need an implementation, which takes as input some regular expression R expressing some regular language L(R), and a string s, and returns accept if \(s\in L(R)\) or reject otherwise.
• We use Finite Automata for this
• A finite automaton consists of
  1. An input alphabet \(\Sigma\)
  2. A finite set of states \(S\)
  3. A start state \(n\)
  4. A set of accepting states \(F \subseteq S\)
  5. A set of transitions state ->input-> state
     • state ->a-> state: In state s1 on input a go to state s2
     • If end of input and in accepting state, then accept
     • Otherwise, reject

Examples

A finite automaton that accepts only 1's

	0	1
A(start)	-	B
B(accept)	-	-

accept any number of 1's followed by a single 0

	0	1
A(start)	B	A
B(accept)	-	-

What does the following DFA accept?

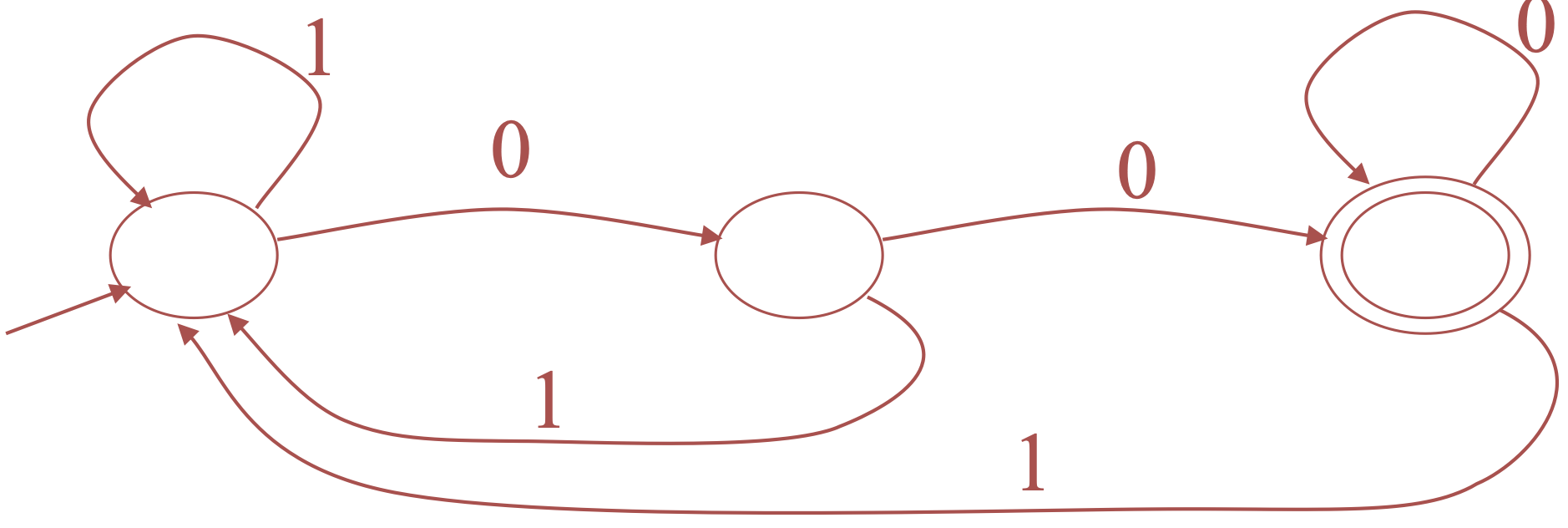- Sol: accepts all strings ending in 00, i.e., the regular language (0+1)* 00

Deterministic Finite Automata (DFA) vs Non-Deterministic Finite Automata (NFA)

• \(\epsilon\)-move

  • Automaton can choose to (1) stay or (2) take \(\epsilon\)-move (move to a diff state but do not consume an input)

• Differences btw DFA and NFA

  DFA	NFA
  One transition per input per state	Multiple transitions for one input in a given state
  No ϵ-moves	Can have ϵ-moves
  One path through the state graph	Multiple paths through the state graph
  Each transition results in one state	A transition can result in a set of states (if any is final at the end of the input, accept. O.W, reject)
  Faster to execute	Slower (exponentially) to execute
  Exponetially large	Exponentially smaller

• Theoretically, DFA and NFA have the same power, i.e., whatever can be done by one can also be achieved by other. Moreover, DFA, NFA, RE are all the same, for every DFA/NFA, there's an equivalent NFA/DFA and equivalent RE, and vice versa.

RE to NFA

• The lexical analysis phase internally performs the following conversion to decide whether a given Cool program has tokens accepted by Cool's lexical specifications (and if not, produce an error).

  Lexical Specs -> RE -> NFA -> DFA -> Table-Driven Implementation of DFA
  

• For every RE, we define an equivalent NFA

  • For \(\epsilon\)

    

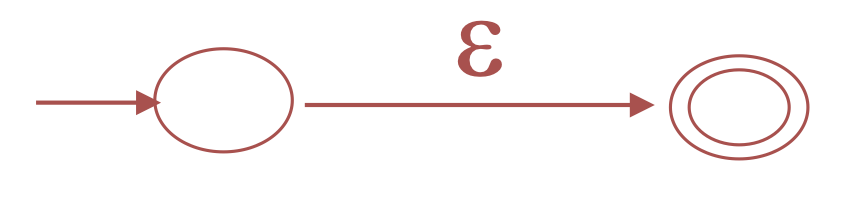
  • For \(a\)

    

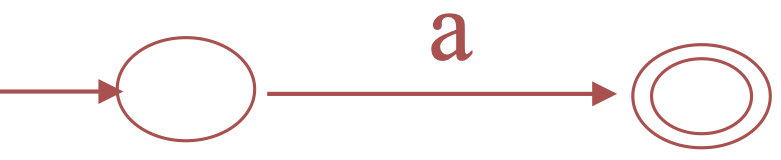
  • For \(AB\)

    

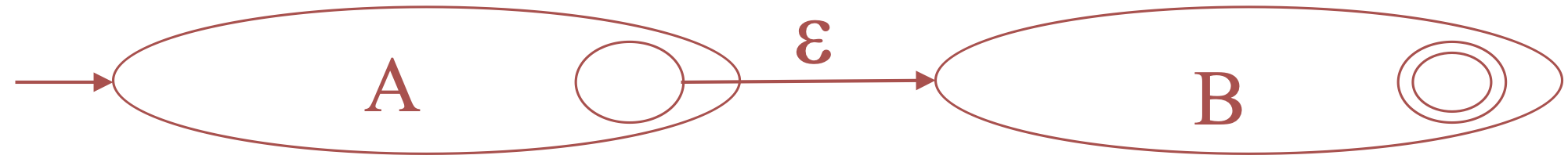
  • For \(A+B\)

    

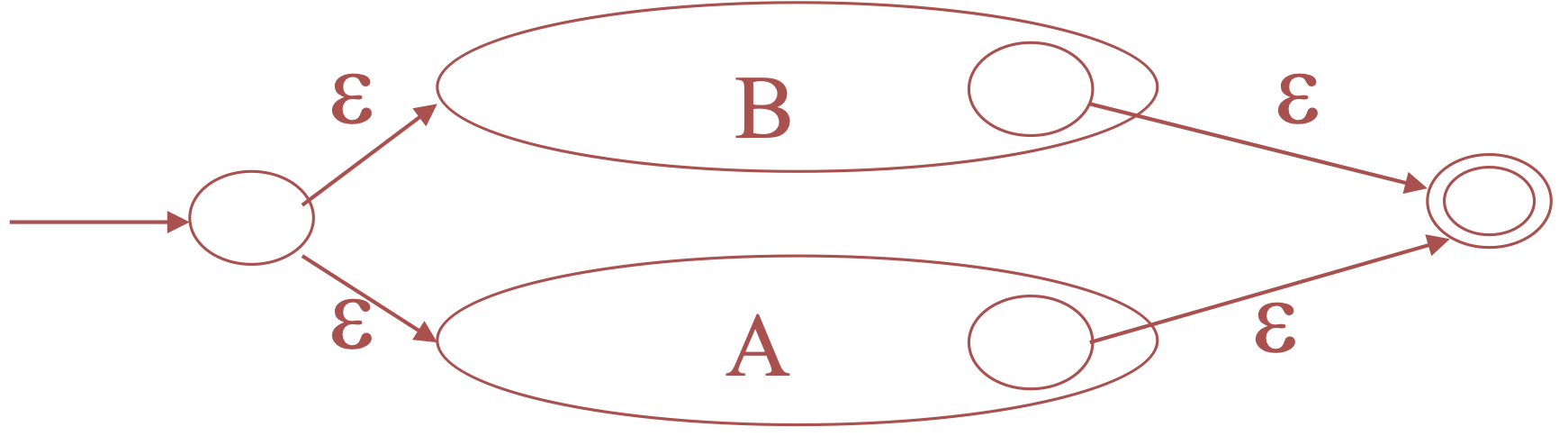
  • For \(A^*\)

    

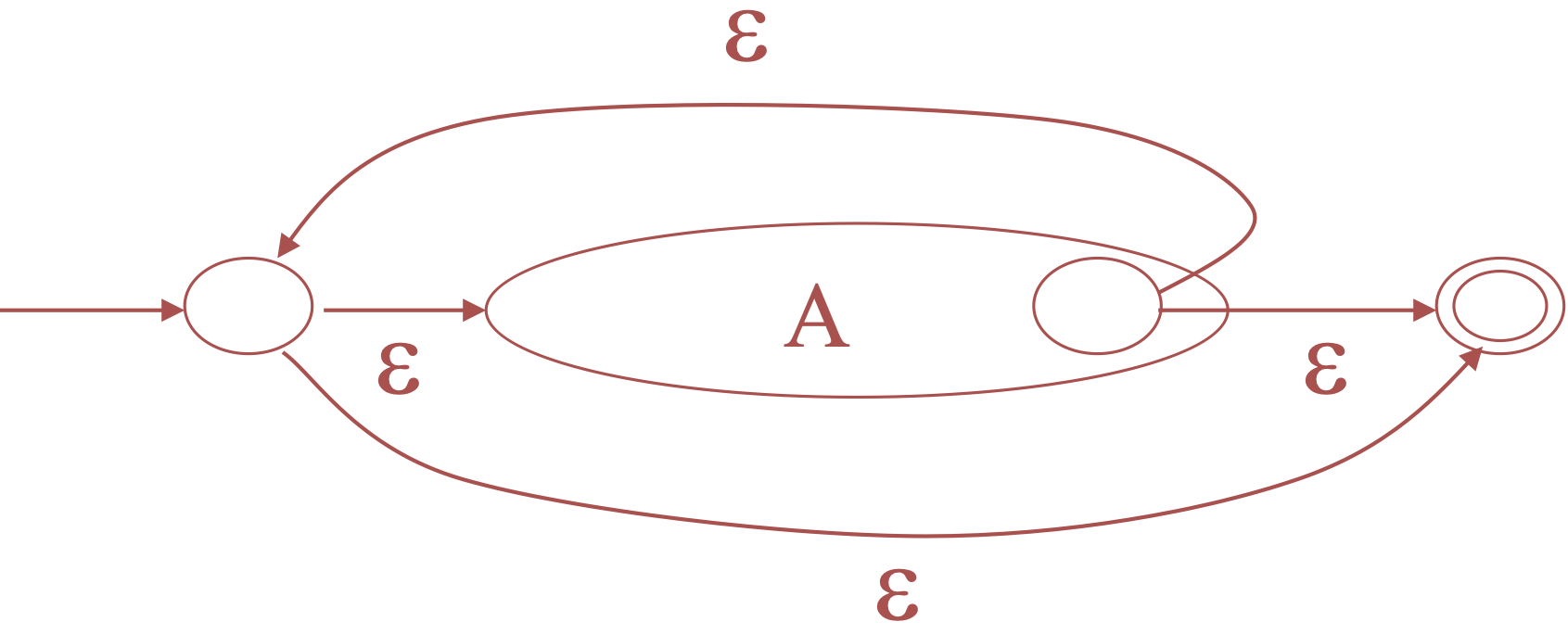
convert the RE \((1+0)*1\) to an NFA

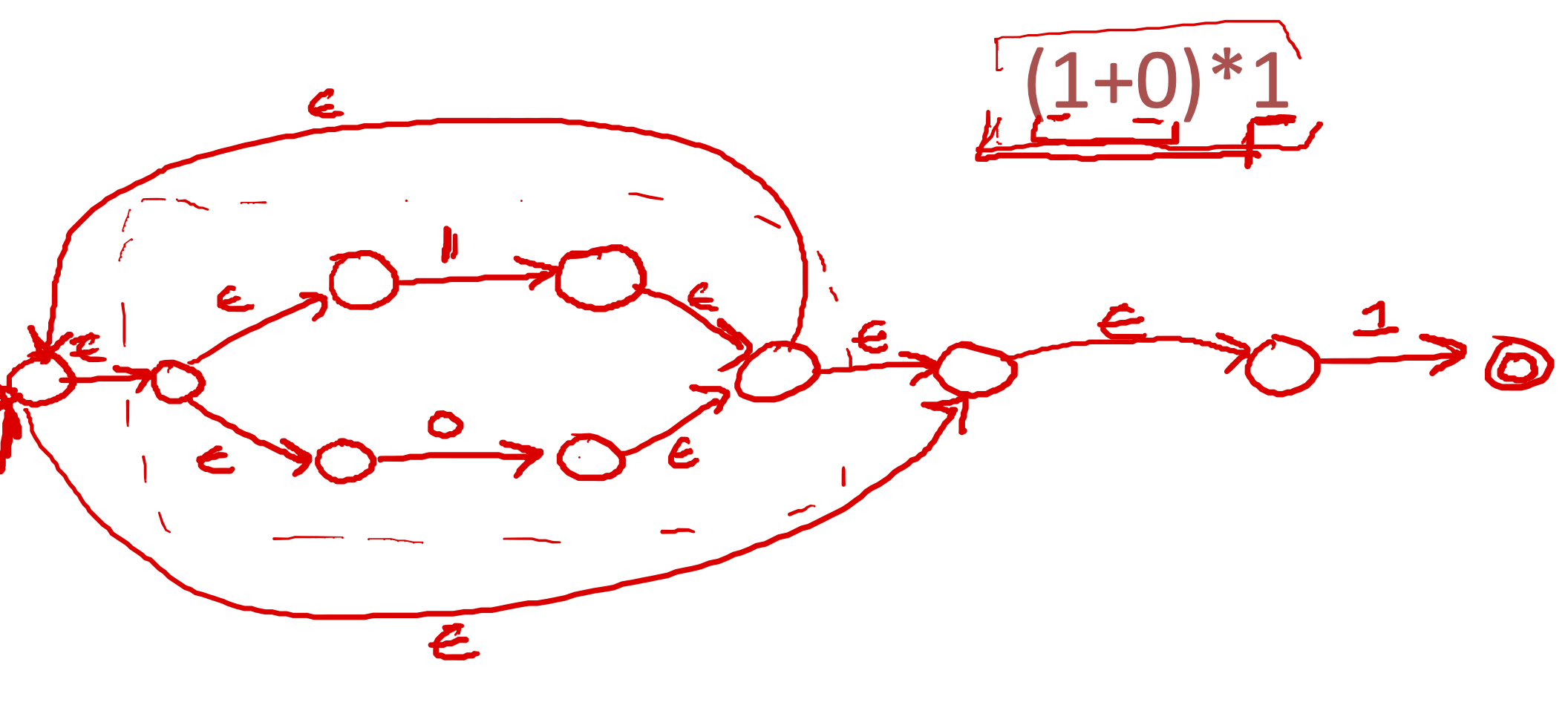
NFA to DFA

• After converting RE to NFA, the lexer internally converts from an NFA to DFA
• For an NFA with n states, each state can go to at most n states, and there are \(2^n-1\) possible non-empty subsets of states (or configurations).

• Converting an NFA with n states can produce a DFA with \(2^n-1\) states

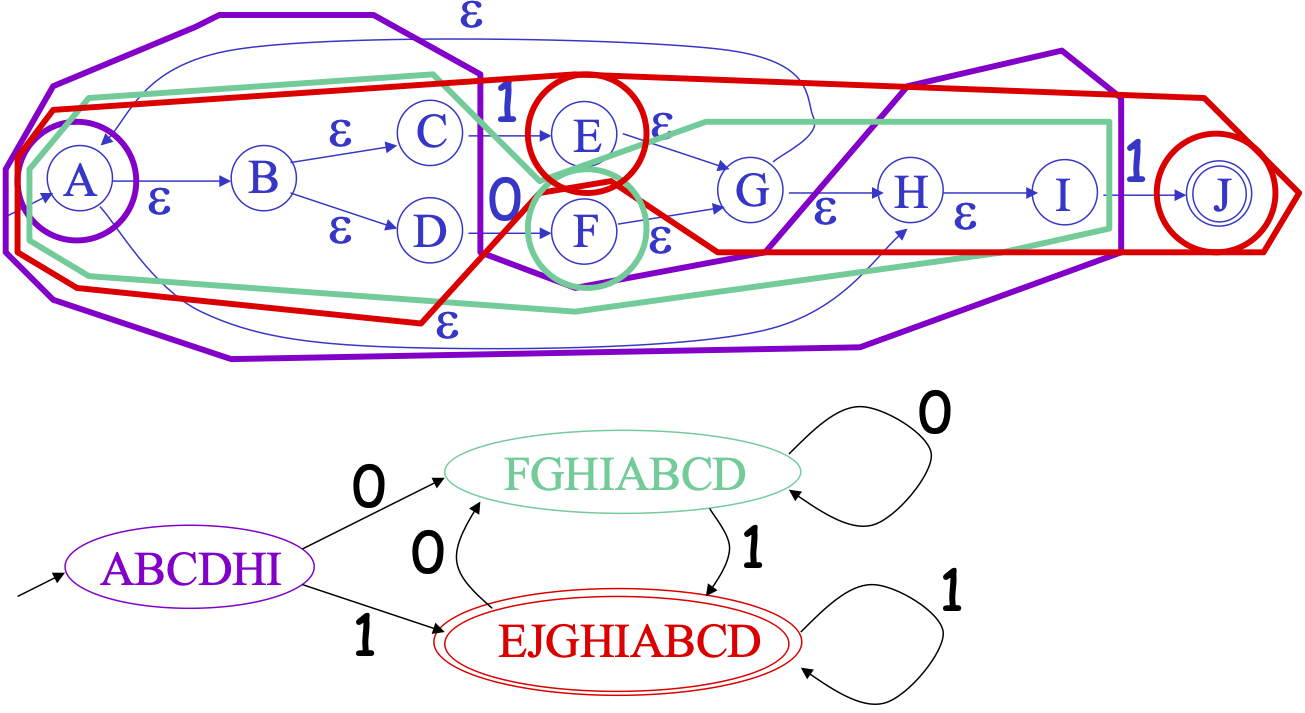
• Consider the example

  

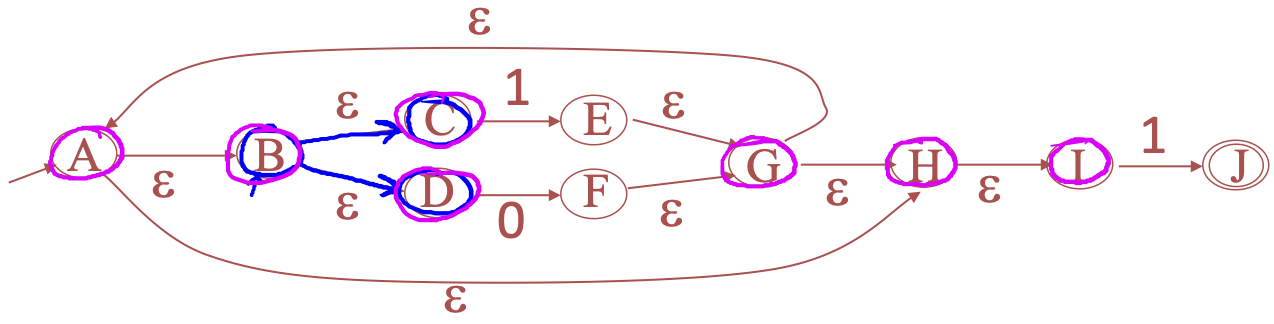
• \(e\)-closure

  • For the above example, the E-clos(B) = {B,C,D} and E-clos(G) = {A,B,C,D,G,H,I}

Converting from an NFA to a DFA

The Structures of a Cool program

• A Cool program

  • Single file (e.g., file.cl)
  • A list of classes
  • 1 of them has to be Main class with a special method main
  • All code must be inside classes (e,g., no global)
  • Can be defined in any order
  • Top-level (no nesting)

  Example

      class Main {
      main() : Object {
          0
          };
      };
  
      class C1 {
      };
  
      class C2 {
      };
  

• A Cool class

  • A list of features
  • features are either attributes or method
  • Attributes are private
  • Methods are public

  Example

      class C inherits IO{
          x: Int;           (* no intializer, default to 0 *)
          y: Bool <- false; (* initialize y to false *)
  
          getx(): Int {x};
          gety(): Bool {y};
  
          print(): Object {
              {
                  out_int(getx());
                  out_string("\n");
                  if y then out_string("true") else out_string("false") fi;
                  out_string("\n");
              }
          };
      };
  
      class Main {
          c : C;
          main(): Object{
              {
                  c <- new C;
                  c.print();
              }
          };
      };
  

• Cool types and inheritance

  • "Primitive" boxed types

    1. Int (default 0)
    2. Bool (default false)
    3. String (default empty string)

  • Other types

    • Main: Boilerplate for code entry
    • IO: inherit this for I/O function
    • Object: Everything inherits Object

  • Type heriachy

    • Object
      • Int : primitive (can't inherit)
      • Bool: primitiv (can't inherit)
      • String: primitiv (can't inherit)
      • Main
      • IO
      • Class A
        • class C (inherits A)
        • ...
      • Class B

  Warning

  • no multiple inheritance (e.g., C cannot inherits from both A and B)
    • can only inherit 1 class at a time (e.g., C inherits A or B)
  • no inheritence cycles (e.g., cannot have A inherits C, B inherits A, and C inherits A
    • How to detect something like this ? in semantics phase !
  • no attribute redefinition
    • E.g., class C has attribute x, and class D inherits C, then D cannot define x
  • cannot have signature change
    • E.g., class C has method m that returns a type T, if D inherits C and override m, then m cannot have a diff return type

• Cool expressions

  • Cool has no statements, only expression
    • expressions have types (e.g., 3 is type Int)

  • Every method contains exactly one expression

    • a block of expressions is also an expression
    • so if want to write lots of expressions, write them in a block

  • Popular expressions in Cool

    • Constaints: 1, true, "Hello"
    • Arithmetic: 1+2 , 3*5
    • Identifiers: x
    • Assignment: x <- expr
    • Comparison: x < 2
    • Conditional: if expr then expr2 else expr3 fi
    • Loop: while expr loop expr1 pool
    • Blocks: {e1, e2, .. , en}
    • Let ..
    • Case .. ...

• Built-in Methods

  • IO:
  • inherit for access to methods such as out_string, out_int

• Dispatch

  • i.e., Method calls
  • 3 types of dispatch: Self, Dynamic, Static