Skip to content

RS1: Regular Languages and Finite Automata

This Review Set asks you questions on regular languages and finite automata. Each of the questions has a short answer. You may discuss the RS with other students and work on the problems together.

Note

For the following, unless specified otherwise, the alphabet is \(\{a, b\}\).

  1. Create DFA's that recognize the following languages.

    1. L1: strings that contain at least one a and an even of b's follow the last a
    2. L2: strings that start and end with the same symbol
    3. L3: strings that contain the string aab as a substring
    4. L4: strings with lengths at most 3

  1. For the following DFA, (1) give a one-sentence description of the language recognized by the DFA and (2) write a regular expression for the same language.

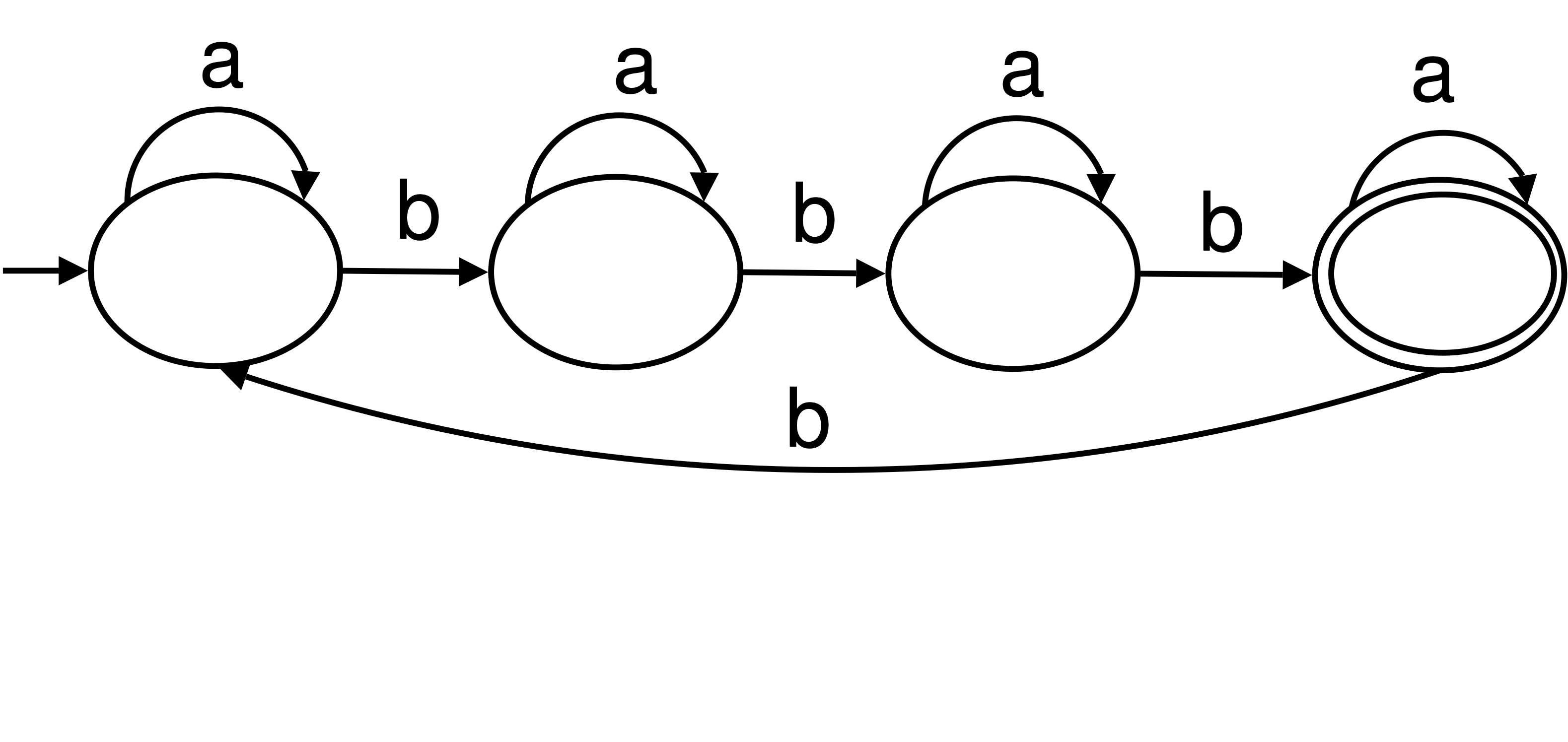
  2. Create an NFA that recognizes the language \(L\) consisting of strings that contain a \(b\) in the 3rd position from the end (e.g., \(aabaa \in L\) but \(aabb \notin L\)).

  3. Convert the following NFA to an equivalent DFA

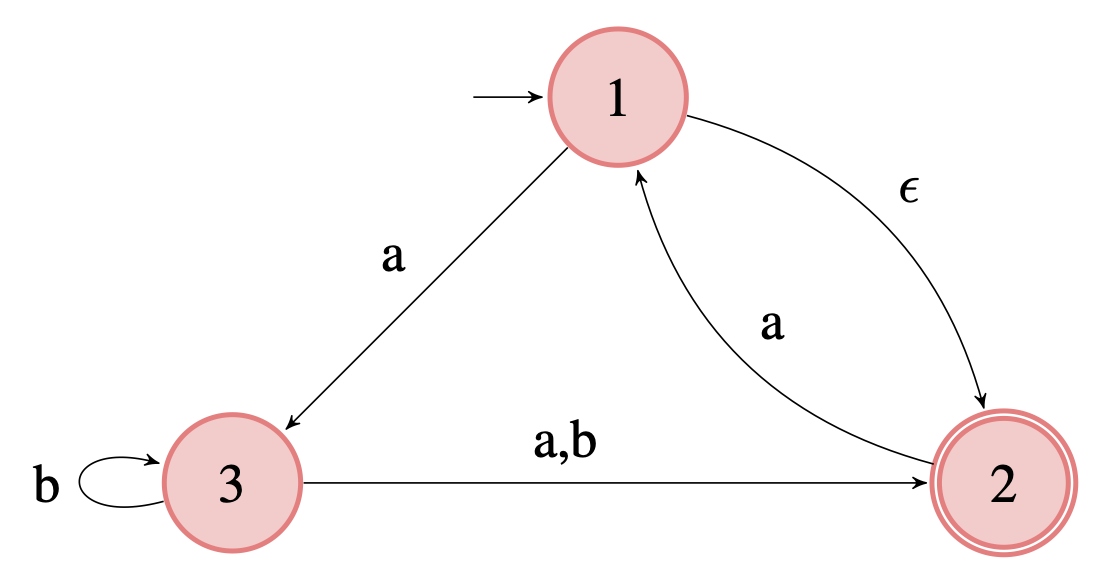
  4. Determine whether or not the following languages are regular. If yes, create a DFA for it. If no, explain in a couple of sentences.

    1. L1 is all strings over the alphabet \(\{(,)\}\) where the parentheses are balanced. For example, \((()(())) \in\) L1 but \((() \notin\) L1.
    2. L2 is all binary representations (i.e., strings over the alphabet \(\{0, 1\}\)) of integers that divisible by 3.
      • Note that the right-most bit of \(w\) is the least-significant bit.
      • For example, the following strings are members of L2: \(\varepsilon\), 0, 11, 110, 1001, 1100, 1111, 10010, 10101, 00, 0011.