Creating and Checking Deep Neural Networks
A simple excercise for creating and checking Deep Neural Networks
1. Goal
First, we manually create standard feedforward neural networks using popular framework such as Tensorflow and Torch. Then, we will check and verify them.
2. Encoding
Consider the following DNN with 2 inputs, 2 hidden layers, and 2 outputs.
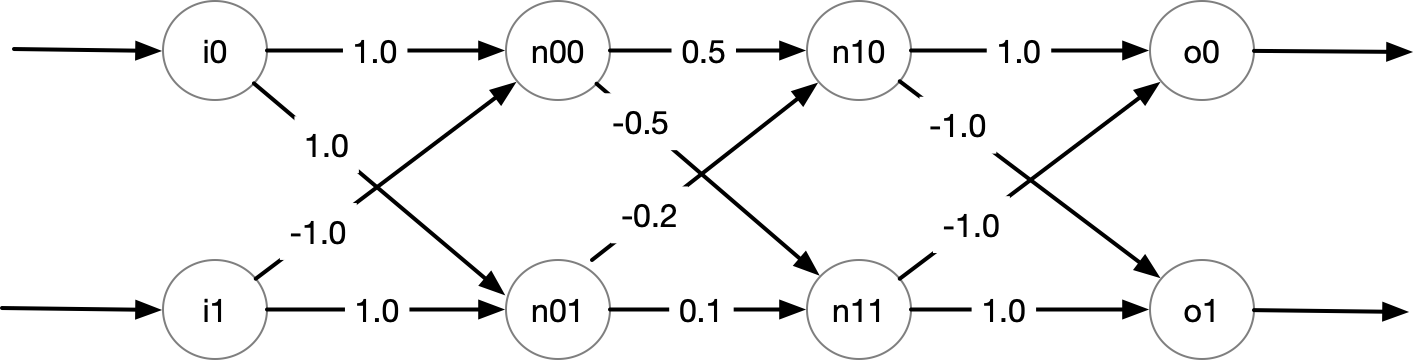
In addition, for this DNN, the outputs of the neurons in the hidden layers (prefixed
with n) are applied with the relu activation function, but the
outputs of the DNN (prefixed with o) are not. These settings are
controlled by the True, False parameters as shown in the code below. Also, this
example does not use bias, i.e., bias values are all 0.0's as shown below.
Note that all of these settings are parameterized and I deliberately use
this example to show these how these parameters are used (e.g., relu
only applies to hidden neurons, but not outputs).
Using Tensorflow:
We can encode this DNN using Tensorflow Keras:
import tensorflow as tf from tensorflow import keras from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras import activations model = Sequential() # layer 0: nodes n00, n01 model.add(Dense(units=2, input_shape=(2, ), # 2 inputs (i.e., i0, i1 in the Figure) activation=activations.relu, # relu activation kernel_initializer=tf.constant_initializer( [[1.0, 1.0], # weights of n00 [-1.0, 1.0] # weights of n01 ]), bias_initializer=tf.constant_initializer( [[0.0], # bias of n00 [0.0]] # bias of n01 ), dtype='float64' )) # layer 1: nodes n10, n11 model.add(Dense(units=2, activation=activations.relu, kernel_initializer=tf.constant_initializer( [[0.5, -0.5], [-0.2, 0.1]]), bias_initializer=tf.constant_initializer([[0.0], [0.0]]), dtype='float64' )) # last layer: nodes represent outputs o0, o1 model.add(Dense(units=2, activation=None, # no activation function for output nodes kernel_initializer=tf.constant_initializer( [[1.0, -1.0], [-1.0, 1.0]]), # weights of o0, o1 bias_initializer=tf.constant_initializer([[0.0], [0.0]]), # bias of o0, o1 dtype='float64' ))
- Using Torch
2.1. Another example
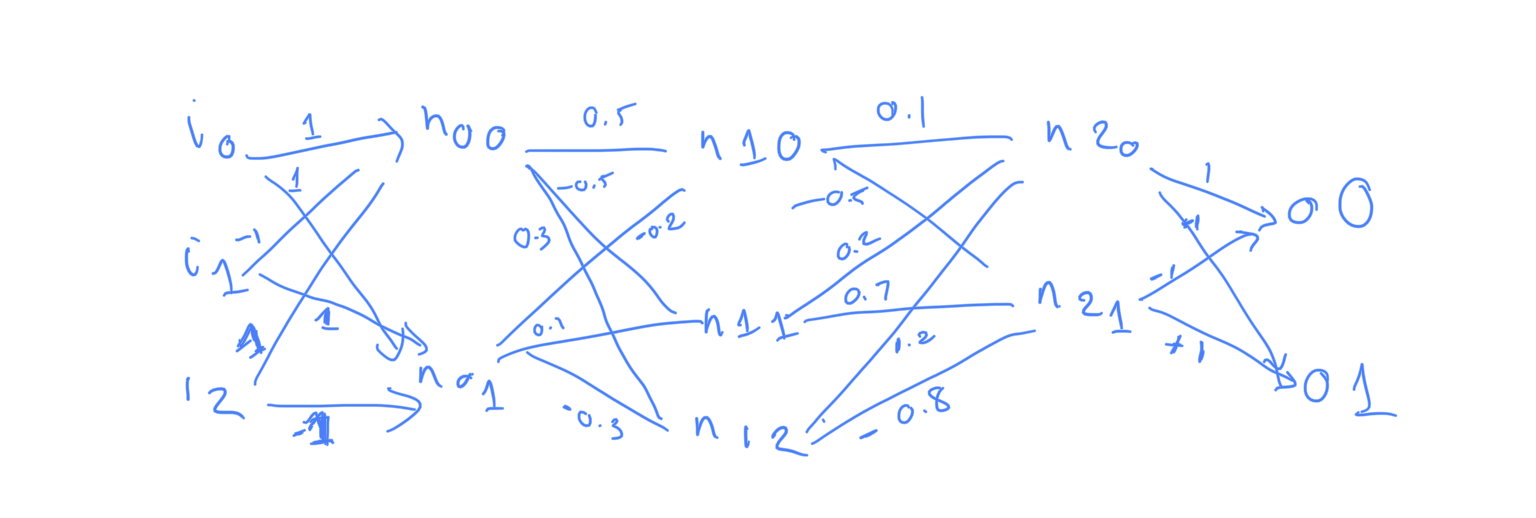
model = Sequential() # n00, n01 d0 = Dense(units=2, input_shape=(3, ), activation=activations.relu, kernel_initializer=tf.constant_initializer( [[1.0, 1.0], [-1.0, 1.0], [1.0, -1.0]]), bias_initializer=tf.constant_initializer( [[0.0], [0.0]]), dtype=dtype) model.add(d0) # n10,n11,n12 d1 = Dense(units=3, activation=activations.relu, kernel_initializer=tf.constant_initializer( [[0.5, -0.5, 0.3], [-0.2, 0.1, -0.3]]), bias_initializer=tf.constant_initializer([[0.0], [0.0], [0.0]]), dtype=dtype ) model.add(d1) # n20, n21 d2 = Dense(units=2, activation=activations.relu, kernel_initializer=tf.constant_initializer( [[0.1, -0.5], [0.2, 0.7], [1.2, -0.8]]), bias_initializer=tf.constant_initializer([[0.0], [0.0]]), dtype=dtype ) model.add(d2) # o0, o1 d3 = Dense(units=2, activation=None, kernel_initializer=tf.constant_initializer( [[1.0, -1.0], [-1.0, 1.0]]), bias_initializer=tf.constant_initializer([[0.0], [0.0]]), dtype=dtype ) model.add(d3)
3. Symbolic Execution
After performing symbolic execution on dnn, we obtain
symbolic states, represented by a logical formula relating inputs and
outputs.
# my_symbolic_execution is something you implement, # it returns a single (but large) formula representing the symbolic states. symbolic_states = my_symbolic_execution(dnn) ... "done, obtained symbolic states for DNN with 2 inputs, 4 hidden neurons, and 2 outputs in 0.1s" assert z3.is_expr(symbolic_states) #symbolic_states is a Z3 formula/expression print(symbolic_states) # And(n0_0 == If(i0 + -1*i1 <= 0, 0, i0 + -1*i1), # n0_1 == If(i0 + i1 <= 0, 0, i0 + i1), # n1_0 == # If(1/2*n0_0 + -1/5*n0_1 <= 0, 0, 1/2*n0_0 + -1/5*n0_1), # n1_1 == # If(-1/2*n0_0 + 1/10*n0_1 <= 0, 0, -1/2*n0_0 + 1/10*n0_1), # o0 == n1_0 + -1*n1_1, # o1 == -1*n1_0 + n1_1)
We can use a constraint solver such as Z3 to query various things about this DNN from the obtained symbolic states:
Generating random inputs and obtain outputs
z3.solve(symbolic_states) [n0_1 = 15/2, o1 = 1/2, o0 = -1/2, i1 = 7/2, n1_1 = 1/2, n1_0 = 0, i0 = 4, n0_0 = 1/2]
Simultating a concrete execution
i0, i1, n0_0, n0_1, o0, o1 = z3.Reals("i0 i1 n0_0 n0_1 o0 o1") # finding outputs when inputs are fixed [i0 == 1, i1 == -1] g = z3.And([i0 == 1.0, i1 == -1.0]) z3.solve(z3.And(symbolic_states, g)) # we get o0, o1 = 1, -1 [n0_1 = 0, o1 = -1, o0 = 1, i1 = -1, n1_1 = 0, n1_0 = 1, i0 = 1, n0_0 = 2]
Checking assertions
print("Prove that if (n0_0 > 0.0 and n0_1 <= 0.0) then o0 > o1") g = z3.Implies(z3.And([n0_0 > 0.0, n0_1 <= 0.0]), o0 > o1) print(g) # Implies(And(i0 - i1 > 0, i0 + i1 <= 0), o0 > o1) z3.prove(z3.Implies(symbolic_states, g)) # proved print("Prove that when (i0 - i1 > 0 and i0 + i1 <= 0), then o0 > o1") g = z3.Implies(z3.And([i0 - i1 > 0.0, i0 + i1 <= 0.0]), o0 > o1) print(g) # Implies(And(i0 - i1 > 0, i0 + i1 <= 0), o0 > o1) z3.prove(z3.Implies(symbolic_states, g)) # proved print("Disprove that when i0 - i1 >0, then o0 > o1") g = z3.Implies(i0 - i1 > 0.0, o0 > o1) print(g) # Implies(And(i0 - i1 > 0, i0 + i1 <= 0), o0 > o1) z3.prove(z3.Implies(symbolic_states, g)) # counterexample # [n0_1 = 15/2, # i1 = 7/2, # o0 = -1/2, # o1 = 1/2, # n1_0 = 0, # i0 = 4, # n1_1 = 1/2, # n0_0 = 1/2]